Human blood is a testament to life’s origin in the OCEAN: its chemical composition is nearly identical to that of sea-water
ATOMIC STRUCTURE
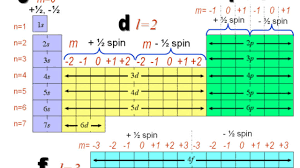
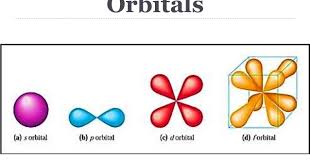
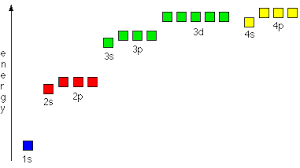
The Energy Shells (n = 1, 2, 3 ….) are divided into energy Sub-shells (l ), which, in turn, are divided into Orbitals (s, p, d, f). Note that the number of sub-shells is determined by the Azimuthal Quantum Number, l, which takes values from 1, 2, …., n. And the number of Orbitals is determined by the Magnetic Quantum Number, ml, which takes values from 1 to (2l – 1).
Note: Conventionally, l is denoted as taking values from 0 to n-1, and ml as taking values from -l to +l.
Illustration:
n=1, so
No. of sub-shells = l = {1} = {s}
No. of orbitals in the one & only sub-shell = 2l-1 = 1 = s
n=2, so
No. of sub-shells = l = {1, 2} = {s, p}
No. of orbitals in 1st sub-shell, s = 1
No. of orbitals in 2nd sub-shell, p = 2l-1 = 2*2 – 1 = 3 = {px, py, pz}
n = 3, so
No. of sub-shells = l = {1, 2, 3} = {s, p, d}
No. of orbitals in 1st sub-shell, s = 1
No. of orbitals in 2nd sub-shell, p = 3
No. of orbitals in 3rd sub-shell, d = 2l-1 = 2*3 – 1 = 5 = {dxy, dxz, dyz, dz2, dx2-y2}
For a detailed study, visit this page. Some extracts from this page are as follows:
The three quantum numbers, n, l, and ml, are properties of specific atomic orbitals that also define in what part of the space an electron is most likely to be located. Orbitals are a result of solving the Schrödinger equation for electrons in atoms. The electron spin is a different kind of property. It is explained by the spin quantum number, or ms. It is a completely quantum phenomenon with no analogues in the classical realm. In addition, it cannot be derived from solving the Schrödinger equation and is not related to the normal spatial coordinates. Electron spin describes an intrinsic electron “rotation” or “spinning.” Each electron acts as a tiny magnet with dipole moment or a tiny rotating object with an angular momentum, even though this rotation cannot be observed in terms of the spatial coordinates.
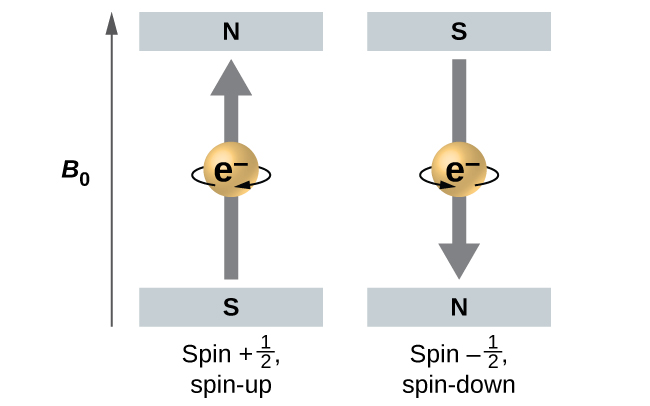
The magnitude of the overall electron spin can only have one value, and an electron can only “spin” in one of two quantized states. One is termed the α state, with the z component of the spin being in the positive direction of the z axis. This corresponds to the spin quantum number ms=1/2. The other is called the β state, with the z component of the spin being negative and ms=−1/2. Any electron, regardless of the atomic orbital it is located in, can only have one of those two values of the spin quantum number. The energies of electrons having ms=−1/2 and ms=1/2 are different if an external magnetic field is applied.
In other words, an electron acts like a tiny magnet. Its moment is directed up (in the positive direction of the z axis) for the 1/2 spin quantum number and down (in the negative z direction) for the spin quantum number of −1/2. A magnet has a lower energy if its magnetic moment is aligned with the external magnetic field (the left electron) and a higher energy if its magnetic moment is opposite to the applied field. A spectral line corresponding to a transition for electrons from the same orbital but with different spin quantum numbers has two possible values of energy; thus, the line in the spectrum will show a fine structure splitting.
(see the Alpha & Beta states animation below).
Next, let us discuss the Quantum Angular Momentum. For a detailed study, visit this page. Some extracts from this page are as follows:
Both the angular momentum and the energy of an atom remain constant if the atom is left undisturbed. Any physical quantity which is constant in a classical system is both conserved and quantized in a quantum mechanical system. Thus both the energy and the angular momentum are quantized for an atom.
There is this Azimuthal Quantum number, denoted by l, which governs the magnitude of the angular momentum, just as the Principal Quantum number n determines the energy. The magnitude of the angular momentum may assume only those values given by: |L| = √l*(l+1)*ℏ, with l = 0, 1, 2, 3, … n−1
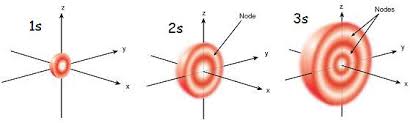
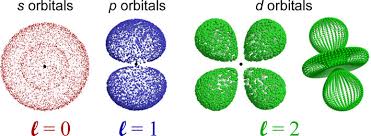
States of zero angular momentum are called s orbitals, which predict spherical density distributions for the electron. As n increases the average value of “r” increases (Recall that the classical physics formula for Angular Momentum is |L⃗| = mνr.). This agrees with the fact that the energy of the electron increases as n increases. The increased energy results in the electron being pulled further away from the attractive force of the nucleus.
As in the simple example of an electron moving on a line, nodes (values of r for which the electron density is zero) appear in the probability distributions. The number of nodes increases with increasing energy and equals n−1.
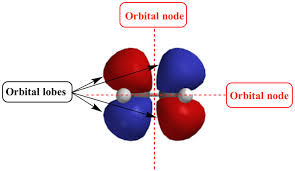
When the electron possesses angular momentum, the density distributions are no longer spherical. In fact for each value of l, the electron density distribution assumes a characteristic shape.
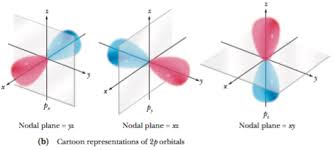
When l=1l=1, the orbitals are called p orbitals. In this case the orbital and its electron density are concentrated along a line (axis) in space. The 2p orbital or wave function is positive in value on one side and negative in value on the other side of a plane which is perpendicular to the axis of the orbital and passes through the nucleus. The orbital has a node in this plane, and consequently an electron in a 2p orbital does not place any electronic charge density at the nucleus. The electron density of a 1s orbital, on the other hand, is a maximum at the nucleus. The same diagram for the 2p density distribution is obtained for any plane which contains this axis. Thus in three dimensions the electron density would appear to be concentrated in two lobes, one on each side of the nucleus, each lobe being circular in cross section.
ENERGY-LEVEL TRANSITION
Everything in the Universe likes to be in its lowest possible energy state or in the Ground state. Electrons in the outermost shell of an atom are loosely bound. If imparted with right amount of energy, they can be made to jump to a higher energy shell. However, the electron will stay in the “excited” or “higher energy” state only for a short time, and will jump back to its Ground state or the previous energy state by releasing or “returning back” the extra energy (the jump to higher energy levels and back to lower energy levels can happen in more complex ways). The amount of energy imparted to or released back by the electron are studied by a spectrometer to measure the changes in energy levels.
The simpler the atoms, the less will be the amount of energy required for such transitions. And less energy means emissions of longer wavelengths, which usually fall in the visible spectrum of EM band. Hence, spectroscopy analysis with atoms of Periods 1 and 2 is easy, as the energy imparted or emitted falls in the category of visible light. However, with atoms of higher atomic number, the energy emitted cannot be seen. It needs to be analysed by other means.
ORBITAL HYBRIDIZATION
likes
MOLECULAR ORBITAL THEORY
likes
ELECTRON BAND THEORY OF SOLIDS
The
SPECTROSCOPY
INTERACTION WITH LIGHT
When light falls onto an atom the oscillations of the electromagnetic wave causes the electron to oscillate. In this fashion the atom absorbs the energy of the light. If this atom now interacts with other atoms it can pass along the photon energy (wave oscillations). This can happen in several different scenarios. One of these is that the energy is passed on without any loss. This is clearly an ideal 100% reflection or a 100% ideal transmission. In another scenario some of the light’s energy could be “used” before it is transmitted to the next atom. This scenario clearly represents absorptionfollowed by reflection/ transmission. But what happens to light when it falls onto an isolated atom? The answer to this question, turns out, to be totally anti-intuitive and somewhat beyond the realm of our understanding of macroscopic world. It is answered by quantum physics. It turns out that very small atoms form a bound structure that can absorb energy and still remain a cohesive unit provided that the energy amount is just right. If the energy amount is not of the “correct” value the atom does not absorb it at all. In the context of quantum physics these “correct” energy values create a set of energy quanta (chunks). So, it is said that the atom’s energy are quantized. This is, of course, in contrast to a macroscopic case, say a child on a swing, that could absorb any value energy – any light or any strong push. So, if the photon’s frequency (wavelength) is not just right, the atom totally ignores photon’s presence.
Historically, it was the absorption/emission of light by individual atoms in a vapor that gave the first clues to the quantum nature of atoms. Because the atoms in a vapor tend to be very far away from one another, for all practical purposes they can be considered as isolated atoms. It was observed that when light that included photons of many energies (frequency/wavelength) was shined on an atomic vapor only very specific wavelengths of the light were absorbed. Equally, when the atomic vapor was energised (say by a high voltage source or by collisions with other atoms) it just emitted discrete wavelengths of light. Experiment can be performed easily to see the light emitted from a tube containing hydrogen atoms in a vapor. A diffraction grating is used to separate the light of different wavelength. Notice that there are only three distinct colors (wavelength/frequencies) that are visible. There is not a continuum of colors, as we see being emitted from the sun, for example.
This behaviour is similar to the case of a person climbing a ladder, as opposed to a person going up an inclined slope. The one who goes up a ladder changes its energy in steps (chunks), while the one who is going up the slope changes energy continuously. By jumping down two rung of the ladder, the ladder climber reduces two chunks of its energy. And so on. It turns out that atoms are “ladder climbers”. They change their energies by going from one rung of their energy ladder (a so called energy level) to another rung (another energy level). To go up their energy ladder they absorb energy equal to the difference between the two energy levels. When they jump down from a higher level to a lower one they emit energy equal to the difference between the two levels. This energy exchange could happen by interacting with another atom, or in isolation by emitting or absorbing a photon.
(CREDITS: Prof. Seyffie Maleki)
A spectrometer is any instrument used to probe a property of light as a function of its portion of the electromagnetic spectrum, typically its wavelength, frequency, or energy. The property being measured is usually intensity of light, but other variables like polarization can also be measured. Technically, a spectrometer can function over any range of light, but most operate in a particular region of the electromagnetic spectrum.
A spectroscope is a device that measures the spectrum of light. Early versions had a slit, a prism, and a screen with markings to indicate various wavelengths or frequencies; later versions were calibrated to electronic detectors. Although the apparatus Isaac Newton used in his work on the spectrum of light can be considered a crude spectroscope, it is generally recognized that the spectroscope was invented by Gustav Kirchhoff and Robert Bunsen around 1860.
A spectrograph is an instrument that separates incoming light by its wavelength or frequency and records the resulting spectrum in some kind of multichannel detector, like a photographic plate. Many astronomical observations use telescopes as, essentially, spectrographs.
X-RAY CRYSTALLOGRAPHY
Deciphering the structure of compounds from the diffraction pattern of light (X-rays)
In 1912, Max von Laue, at the University of Munich in Germany, postulated that atoms in a crystal lattice had a regular, periodic structure with interatomic distances on the order of 1 A. Without having any evidence to support his claim on the periodic arrangements of atoms in a lattice, he further postulated that the crystalline structure can be used to diffract x-rays, much like a gradient in an infrared spectrometer can diffract infrared light. His postulate was based on the following assumptions: the atomic lattice of a crystal is periodic, x- rays are electromagnetic radiation, and the interatomic distance of a crystal are on the same order of magnitude as x- ray light. Laue’s predictions were confirmed when two researchers: Friedrich and Knipping, successfully photographed the diffraction pattern associated with the x-ray radiation of crystalline CuSO4⋅5H2O. The science of x-ray crystallography was born.
The arrangement of the atoms needs to be in an ordered, periodic structure in order for them to diffract the x-ray beams (see the video below). A series of mathematical calculations is then used to produce a diffraction pattern that is characteristic to the particular arrangement of atoms in that crystal. X-ray crystallography remains to this day the primary tool used by researchers in characterizing the structure and bonding of organometallic compounds.
(source: https://chem.libretexts.org/Bookshelves/Analytical_Chemistry/Supplemental_Modules_(Analytical_Chemistry)/Instrumental_Analysis/Diffraction_Scattering_Techniques/X-ray_Crystallography)
ok
AMORPHOUS & CRYSTALLINE STRUCTURES
Have
To understand in detail
For Learners:
DIYHA (do it yourself home activity):
Properties of Quantum Numbers
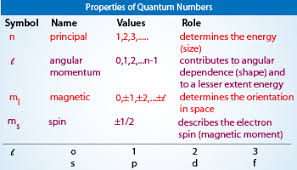
What do they symbolise?
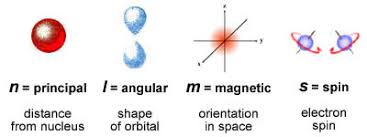
Shapes as per A.M
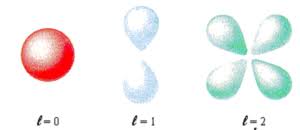
Intrinsic Spin
Q.N in Periodic Table
Discrete positions only
Shapes of spdf orbitals
p Orbitals
p Orbitals along axes
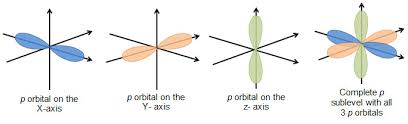
Node areas of zero probability

Alpha & Beta states
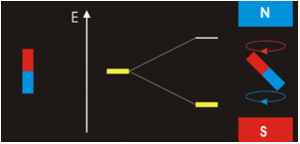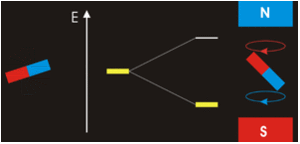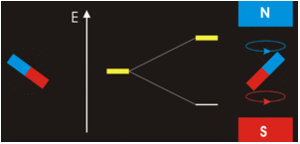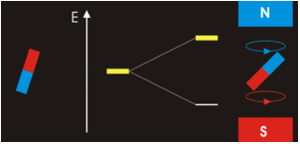
Orbital Nodes
Orbital energy levels
Nodal Planes
Orbital Nodes

QUIZ
Each of the following questions has four answer options: a, b, c, d. Choose the correct one.
1. If you are situated anywhere at the Tropic of Cancer then your shadow can never point in this direction:
(a) North
(b) East
(c) South
(d) West
2. Consider the
